Globe analogy concept
In: Examined planes
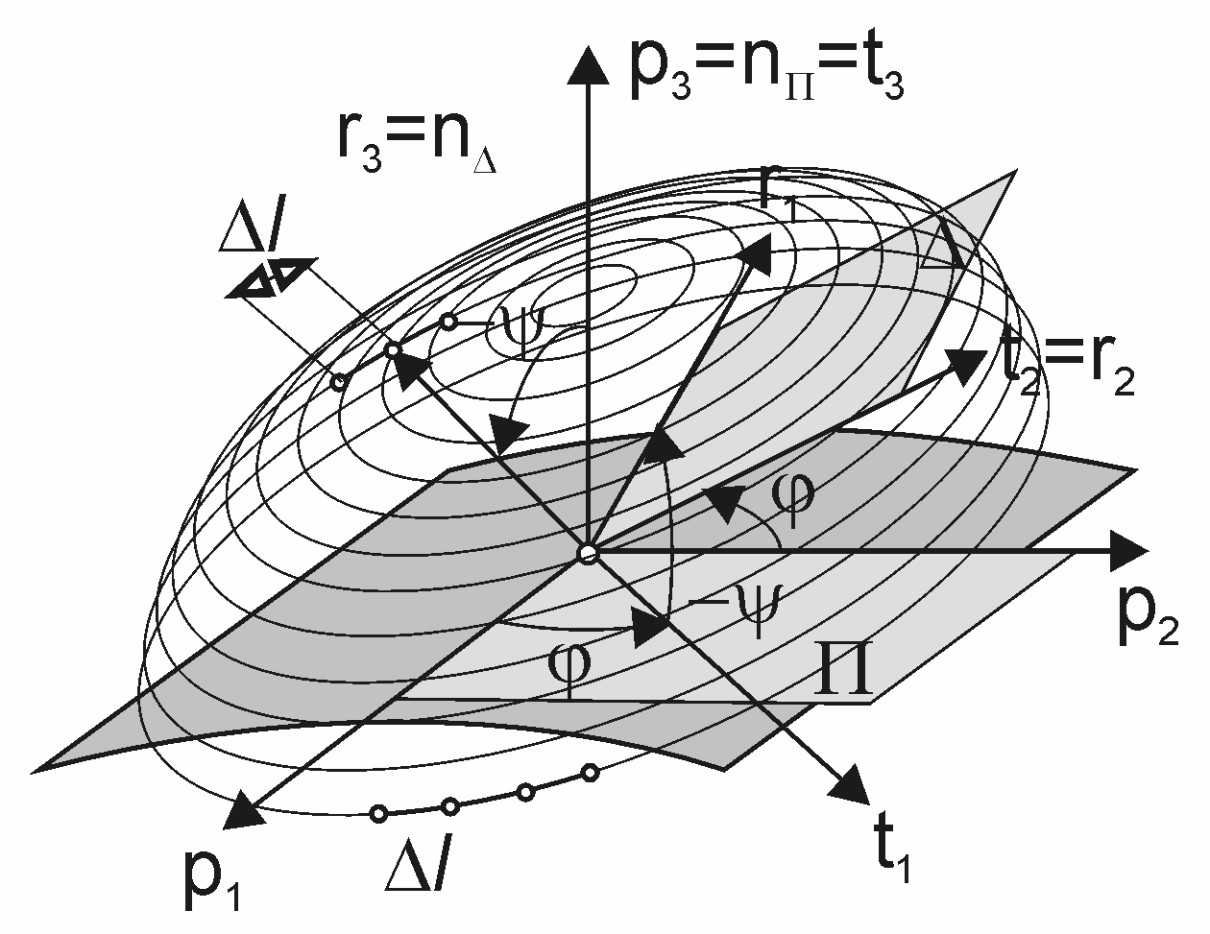
Although far from perfect, the following picture is necessary for description of the globe analogy concept:
There are two coordinate systems depicted. The pi system describes the local coordinate system built in such a way that the p3 axis is the normal line to the surface of the component at the point examined. The second coordinate system marked as ri here is reached by two subsequent rotations of Euler angles 
and 
. The r3 axis corresponds to the normal line of the plane that is currently evaluated whether it is not the critical plane. Since the plane normal and not the whole coordinate system is the necessary output, the third Euler angle is inactive.
The ellipses drawn in the thin line are in the picture in order to describe chosen potential course of an end point of the rotating r3 normal line if “all” possible planes have to be evaluated in a discrete manner. Well, naturally if seen from the p3 direction, they should be circles – the picture is not so fine as I hoped. These are the meridians of the globe – that’s why it is called globe analogy concept. Only one hemisphere is examined, because of the stress/strain state on the second one is covered with it as well.
Distance between the meridians is indirectly chosen by the user in the Number of scanned planes of the Calculation Methods dialogue. Here the user specifies not complete number of all planes but how many planes will be examined along the equator, which is here the largest circle lying on p1p2 plane – i.e. the angular step of the first Euler rotation. This angular step is the same as regards the second rotation throughout the whole search.
While the angular step of the second rotation is kept, the angular step for move on each meridian differs. That is so because of the fact, that how the longitude increases, the meridian becomes smaller. If the same angular step would be preserved, the small meridians would be described in very high density. This seems to be unnecessary, thus here the idea of preserving the length between two examined point on unit sphere – this is the Δl distance in the picture above.
The quality of such an approach was examined in integral methods, where the discretization of the space plays a very important role. The differences in Papadopoulos or Zenner & Liu method, where the analytical solution was compared, were on the third position of the fatigue index FI, when the number of scanned planes option was set to 180. Nevertheless, no more precise analysis of the influence of angular step was done.
The use of the globe analogy concept is preferred even for critical plane methods by me (Jan Papuga, author). The determination of the normal line to the surface on a discrete complex FE-mesh can be dubious. The deviation from the proper position can significantly affect the results given by Bannantine-Socie concept and the development of the other option - random concept - is not active for some time. The globe analogy concept here allows to lessen the number of scanned planes to lower values, while the option Optimize <1~yes, 0~no> in the Calculation Methods dialogue is switched on.
More:
© PragTic, 2007
This help file has been generated by the freeware version of HelpNDoc